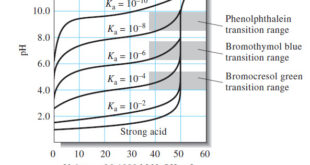
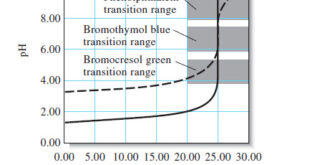
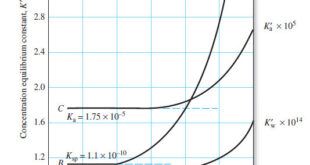
Titration Curves for Weak Acids – Four distinctly different types of calculations are needed to compute values for a weak acid (or a weak base) titration curves: (1) At the beginning, the solution contains only a weak acid or a weak base, and the pH is calculated from the concentration …
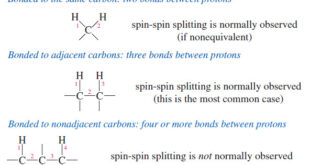
Read More »Spin-Spin Splitting in ¹H NMR Spectra
– In this topic, we will discuss The Spin-Spin Splitting in ¹H NMR Spectra. Theory of Spin-Spin Splitting – A proton in the NMR spectrometer is subjected to both the external magnetic field and the induced field of the shielding electrons. – If there are other protons nearby, their small …
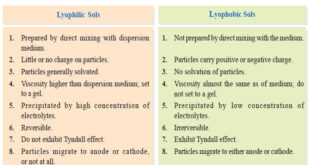
Read More »Lyophilic and Lyophobic sols : Defination, Properties, Comparison
– In this topic, we will discuss The Lyophilic and Lyophobic sols : Defination, Characteristics, and Comparison. Defination of Lyophilic and Lyophobic sols – Sols are colloidal systems in which a solid is dispersed in a liquid. – These can be subdivided into two classes : Lyophilic sols (solvent-loving) Lyophobic …
Read More »Titration of Strong Acids and Bases
– In this topic, we will discuss The Titration of Strong Acids and Bases. Introduction to Titration of Strong Acids and Bases – The hydronium ions in an aqueous solution of a strong acid have two sources: (1) the reaction of the acid with water and (2) the dissociation of …
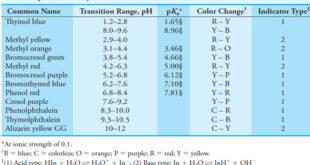
Read More »Indicators and Solutions for acid-base titration
– In this topic, we will discuss the Indicators and Solutions for acid-base titration. Indicators and Solutions for acid-base titration – Like all titrations, neutralization titrations depend on a chemical reaction of the analyte with a standard reagent. – There are several different types of acid/base titrations. – One of …
Read More »Titration Curves in Analytical Chemistry : Definition, Types
– In this topic, we will discuss the Titration Curves in Analytical Chemistry : Definition and Types Titration Curves – An end point is signaled by an observable physical change near the equivalence point of a titration. – The two most widely used signals involve (1) changes in color due …
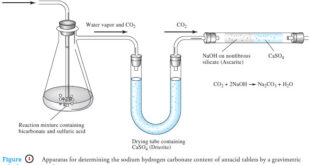
Read More »Gravimetric Titrations | Definition, Calculations & Advantages
Gravimetric titrations – Mass (weight) or gravimetric titrations differ from their volumetric counterparts in that the mass of titrant is measured rather than the volume. – Therefore, in a mass titration, a balance and a weighable solution dispenser are substituted for a buret and its markings. – Gravimetric titrations actually …
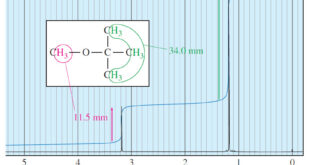
Read More »Areas of the Peaks in NMR Spectroscopy
– In this topic, we will discuss The Areas of the Peaks in NMR Spectroscopy Areas of the Peaks – The area under a peak is proportional to the number of hydrogens contributing to that peak. – For example, in the methyl tert-butyl ether spectrum (Figure 1), the absorption of …
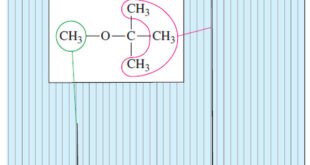
Read More »Number of Signals in NMR Spectroscopy
The Number of Signals – In general, the number of NMR signals corresponds to the number of different kinds of protons present in the molecule. – For example, methyl tert-butyl ether has two types of protons (Figure 1). – The three methoxy protons are chemically identical, and they give rise …
Read More »Colloids: Definition, History and Types
– In this topic, we will discuss the colloids: definition, History and Types History of colloids – Thomas Graham (1861) studied the ability of dissolved substances to diffuse into water across a permeable membrane. – He observed that crystalline substances such as sugar, urea, and sodium chloride passed through the …
Read More »Some Terms Used in Volumetric Titration
Some Terms Used in Volumetric Titration – A standard solution (or a standard titrant) is a reagent of known concentration that is used to carry out a volumetric titration. – The volumetric titration is performed by slowly adding a standard solution from a buret or other liquid dispensing device to …
Read More »Applications of Gravimetric methods
Applications of Gravimetric methods – Gravimetric methods have been developed for most inorganic anions and cations, as well as for such neutral species as water, sulfur dioxide, carbon dioxide, and iodine. – A variety of organic substances can also be determined gravimetrically. – Examples include lactose in milk products, salicylates …
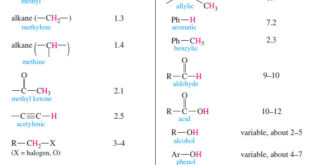
Read More »Chemical Shift in NMR Spectroscopy
– In this topic, we will discuss the Chemical Shift in 1H NMR Spectroscopy. What is Chemical Shift? – The variations in the positions of NMR absorptions, arising from electronic shielding and deshielding, are called chemical shifts. – Chemical shift is The difference (in parts per million) between the resonance …
Read More »Precipitation Gravimetry
– In this topic, we will discuss the Precipitation Gravimetry as an important one of Gravimetric Analysis in analytical chemistry. What is Gravimetric Analysis? – Gravimetric analysis is a method to determine the quantity of an analyte based on the mass of a solid. – Gravimetric methods of analysis are …
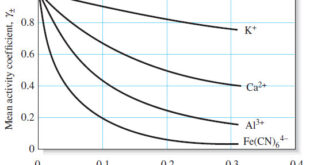
Read More »Activity Coefficients : Definition, Equation, Examples, Properties
– In this topic, we will discuss Activity coefficients : Definition, Equation, Examples and Properties. Activity Coefficients – Chemists use a term called activity, a, to account for the effects of electrolytes on chemical equilibria. – The activity, or effective concentration, of species X depends on the ionic strength of …
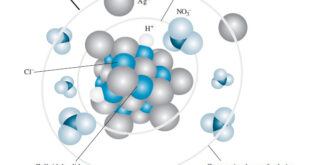
Read More »The Effect of Electrolyte on Chemical Equilibria
The Effect of Electrolyte on Chemical Equilibria – Experimentally, we find that the position of most solution equilibria depends on the electrolyte concentration of the medium, even when the added electrolyte contains no ion in common with those participating in the equilibrium. – For example, consider again the oxidation of …
Read More »What is Analytical Chemistry?
What is Analytical Chemistry? Analytical chemistry is what analytical chemists do. – Analytical chemistry is too broad and active a discipline for us to easily or completely define in an introductory textbook. Instead, we will try to say a little about what analytical chemistry is, as well as a little …
Read More »Acid-Base catalysis (definition – Examples – Mechanism)
– In this topic, we will discuss Acid-Base catalysis: definition, Examples and Mechanism. Acid-Base catalysis – A number of homogeneous catalytic reactions are known which are catalysed by acids or bases, or both acids and bases. These are often referred to as Acid-Base catalysts. – Arrhenius pointed out that acid …
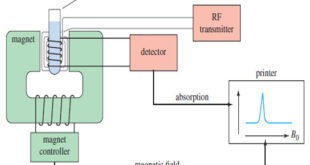
Read More »NMR spectrometer
What happens in an NMR spectrometer? – Before discussing the design of spectrometers, let’s review what happens in an NMR spectrometer. – Protons (in the sample compound) are placed in a magnetic field, where they align either with the field or against it. – While still in the magnetic field, …
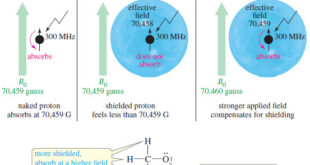
Read More »Magnetic Shielding by Electrons
– In this topic, we will discuss the Magnetic Shielding by Electrons Magnetic Shielding by Electrons – Up to now, we have considered the resonance of a naked proton in a magnetic field, but real protons in organic compounds are not naked. – They are surrounded by electrons that partially …
Read More » Read Chemistry
Read Chemistry